IID test testing

Here we have some examples of the tests that were run against our own IID tests in order to validate them.

Slow permutation test

We created a synthetic entropy file called 10000000.4. This was 10 MB of Python’s Mersenne Twister output with $ H_{\infty} $ = 4 bits/byte. The test was set for a significance threshold (α = 0.01) of 100 normalised test statistic values < 1.0:-

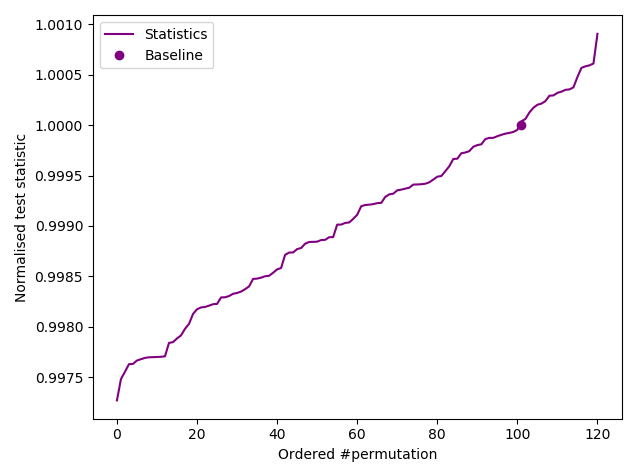
Successful test of 10 MB of Mersenne Twister output.

Successful test of 10 MB of Mersenne Twister output.

10000000.4, with threshold set to 1000:-

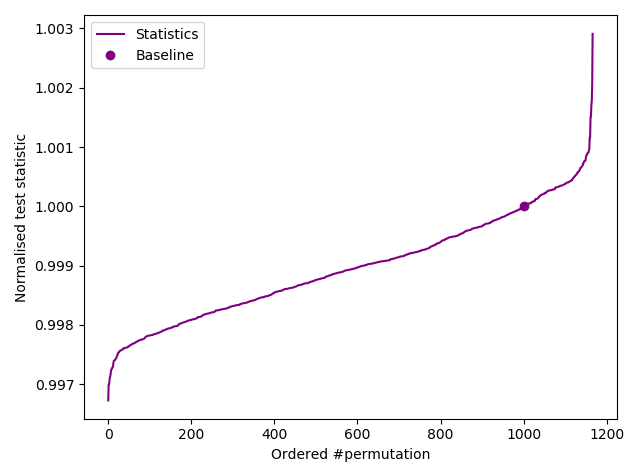
Successful test of 10 MB of Mersenne Twister output.

Successful test of 10 MB of Mersenne Twister output.

And finally slow IID test for 10000000.4 with no threshold, so a full run of 10,000 permutations. This took ~25,000 seconds and completed after more than 8000 normalised test statistics < 1.0:-

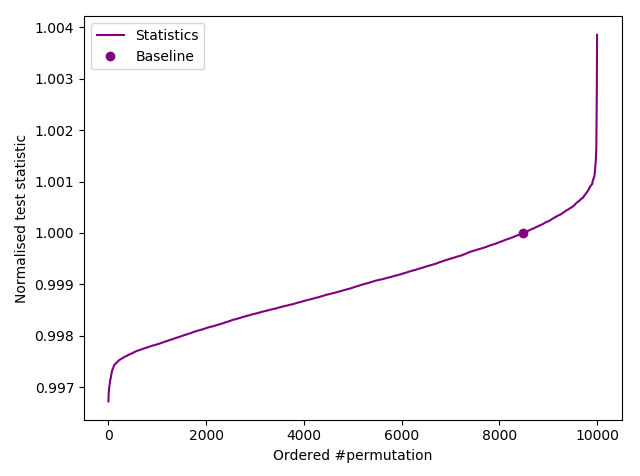
Successful test of 10 MB of Mersenne Twister output.

Successful test of 10 MB of Mersenne Twister output.

Full run results for NIST’s own GitHub example /bin/data.pi.bin which should be IID but clearly isn’t (but only by a little bit (~0.6%) so it’s not an encoding problem). This result indicates a failure and that $H_0$ must be rejected as $C \ngtr 100$. It also fails NIST’s own IID test (curious). What’s it for, and why is the non-IID error so small yet still perfectly and repetitively identifiable by our’s and NIST’s testing? Did they not actually test it for themselves:-

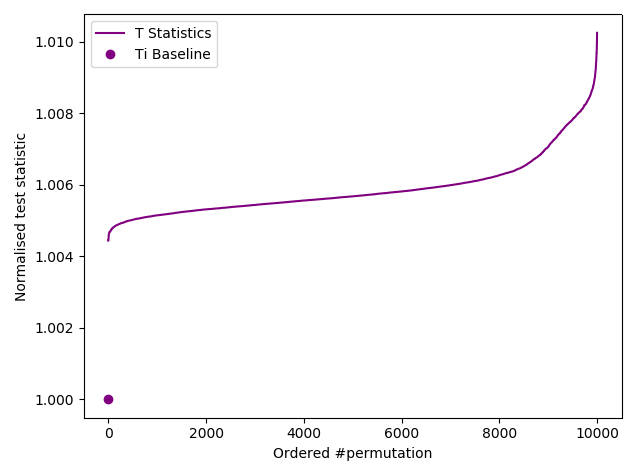
Failed test of NIST's pi.

Failed test of NIST's pi.

We also know that the problem is not a §5.1 Conversion I type error as NIST’s /bin/truerand_1bit.bin test file passes whilst being exactly the same binary format as the pi file. values, counts = np.unique(data, return_counts=True) gives [502694 662972] counts for all [0 1] values. So we find that /bin/data.pi.bin is also biased. They miscalculated the value of pi as we know it to be normal in all bases. Silly, silly NIST.

And as expected, a successful (IID) test run for 10 MB of 8 bit /dev/urandom which took less than 10 minutes to achieve $C \geq 100$, and it’s text output:-

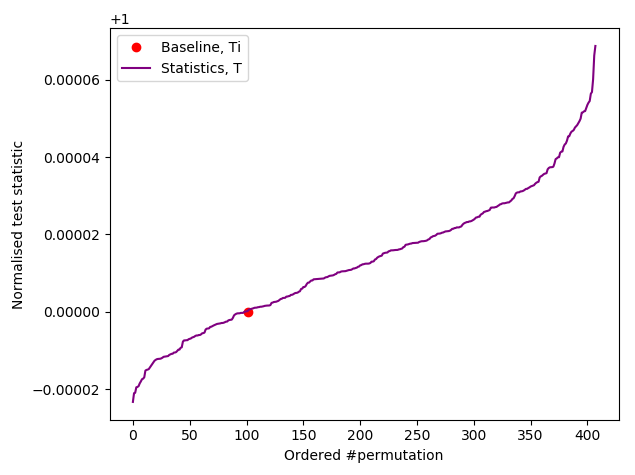
Successful test of 10 MB of /dev/urandom output.

Successful test of 10 MB of /dev/urandom output.

Starting IID test...
Baseline: 40182584
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Compressor Thread-2 started.
Compressor Thread-3 started.
Compressor Thread-1 started.
Compressor Thread-4 started.
Compressor Thread-0 started.
Compressor Thread-1 Permutation 1, Normalised statistic = 1.0000097056973738
Compressor Thread-4 Permutation 1, Normalised statistic = 1.0000326509614215
Compressor Thread-2 Permutation 1, Normalised statistic = 0.9999993031807014
Compressor Thread-3 Permutation 1, Normalised statistic = 0.9999879300942915
Compressor Thread-0 Permutation 1, Normalised statistic = 1.0000025135267558
CURRENT RANK = 2
Compressor Thread-2 Permutation 2, Normalised statistic = 1.0000049523943009
Compressor Thread-4 Permutation 2, Normalised statistic = 1.0000280220903663
Compressor Thread-0 Permutation 2, Normalised statistic = 1.0000198842364145
Compressor Thread-3 Permutation 2, Normalised statistic = 0.9999995769311402
Compressor Thread-1 Permutation 2, Normalised statistic = 1.0000025881859664
CURRENT RANK = 3
Compressor Thread-0 Permutation 3, Normalised statistic = 1.0000476574627455
Compressor Thread-2 Permutation 3, Normalised statistic = 0.9999970882907878
Compressor Thread-3 Permutation 3, Normalised statistic = 1.0000086106956187
Compressor Thread-1 Permutation 3, Normalised statistic = 0.999994475218418
Compressor Thread-4 Permutation 3, Normalised statistic = 1.0000516144009057
CURRENT RANK = 5
Remaining running time to full completion = 20019s
Estimated full completion date/time = 2020-04-03T06:14:40.238931
Compressor Thread-0 Permutation 4, Normalised statistic = 1.0000545261101177
Compressor Thread-4 Permutation 4, Normalised statistic = 1.0000269768614183
Compressor Thread-1 Permutation 4, Normalised statistic = 1.0000026877315804
Compressor Thread-2 Permutation 4, Normalised statistic = 1.0000116966096555
Compressor Thread-3 Permutation 4, Normalised statistic = 0.9999875319118352
CURRENT RANK = 6
Remaining running time to full completion = 20009s
Estimated full completion date/time = 2020-04-03T06:14:40.238931
Compressor Thread-0 Permutation 5, Normalised statistic = 1.0000153300245698
Compressor Thread-4 Permutation 5, Normalised statistic = 1.0000461393921307
Compressor Thread-1 Permutation 5, Normalised statistic = 1.000030908913175
Compressor Thread-2 Permutation 5, Normalised statistic = 1.0000053008039502
Compressor Thread-3 Permutation 5, Normalised statistic = 1.0000519379241515
CURRENT RANK = 6

... snip ...

Remaining running time to full completion = 16005s
Estimated full completion date/time = 2020-04-03T05:18:16.238931
Compressor Thread-4 Permutation 80, Normalised statistic = 1.0000157033206227
Compressor Thread-1 Permutation 80, Normalised statistic = 1.0000066446697404
Compressor Thread-2 Permutation 80, Normalised statistic = 1.0000208796925554
Compressor Thread-0 Permutation 81, Normalised statistic = 1.0000354631250195
Compressor Thread-3 Permutation 81, Normalised statistic = 1.0000093324013208
Compressor Thread-4 Permutation 81, Normalised statistic = 1.000018814121063
Compressor Thread-1 Permutation 81, Normalised statistic = 0.9999956946521906
Compressor Thread-2 Permutation 81, Normalised statistic = 1.0000176195736938
CURRENT RANK = 99
Remaining running time to full completion = 15913s
Estimated full completion date/time = 2020-04-03T05:16:54.238931
Compressor Thread-0 Permutation 82, Normalised statistic = 0.999994425445611
Compressor Thread-3 Permutation 82, Normalised statistic = 1.000017768892115
Compressor Thread-4 Permutation 82, Normalised statistic = 1.0000245877666802
Compressor Thread-1 Permutation 82, Normalised statistic = 0.9999789212162165
Compressor Thread-2 Permutation 82, Normalised statistic = 1.0000187145754489
CURRENT RANK = 101
Remaining running time to full completion = 15945s
Estimated full completion date/time = 2020-04-03T05:17:36.238931

----------------------------------
Ranked as > 101/10,000
*** PASSED permutation test. There is no evidence that the data is not IID ***
Based on 410 permutations.
Test results in file: /tmp/results.json

Fast permutation test

For NIST’s data.pi.bin, where you can see that the compressed permuted size was always bigger than the initial un-permuted compressed sample $ \big( \forall T, ~ \frac{T}{T_i} > 1 \big) $:-

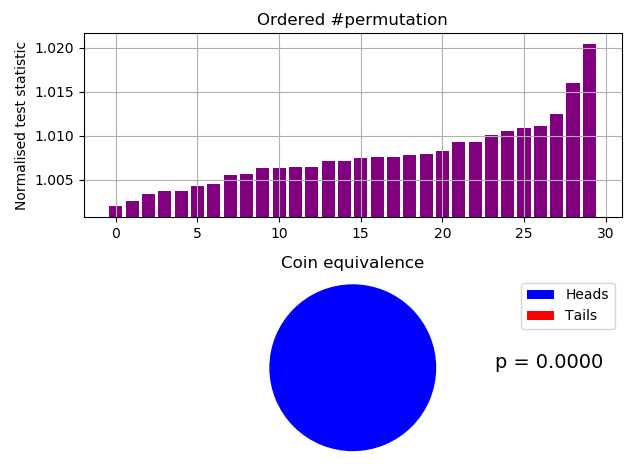
Failed test of NIST's pi.

Failed test of NIST's pi.

LZMA tests...
Permutation 1 : NTS = 1.011061946902655
Permutation 2 : NTS = 1.0075315840621963
Permutation 3 : NTS = 1.0063694267515924
Permutation 4 : NTS = 1.0100638193421698
Permutation 5 : NTS = 1.0105703048180925
Permutation 6 : NTS = 1.0092977734279422
Permutation 7 : NTS = 1.0203881110292312
Permutation 8 : NTS = 1.015990159901599
Permutation 9 : NTS = 1.007113073338239
Permutation 10 : NTS = 1.0125030644765873


BZ2 tests...
Permutation 1 : NTS = 1.0078542780748663
Permutation 2 : NTS = 1.0055769338017957
Permutation 3 : NTS = 1.0020026702269693
Permutation 4 : NTS = 1.0037222222222222
Permutation 5 : NTS = 1.006396707086439
Permutation 6 : NTS = 1.0033405712376817
Permutation 7 : NTS = 1.0045062586926286
Permutation 8 : NTS = 1.0036699288256228
Permutation 9 : NTS = 1.0043297252289758
Permutation 10 : NTS = 1.0026111111111111


ZLIB tests...
Permutation 1 : NTS = 1.006412059170932
Permutation 2 : NTS = 1.0056789429294348
Permutation 3 : NTS = 1.010827271189308
Permutation 4 : NTS = 1.0063483146067416
Permutation 5 : NTS = 1.0079432144667906
Permutation 6 : NTS = 1.0092503807321338
Permutation 7 : NTS = 1.0082123973450332
Permutation 8 : NTS = 1.0075846957694252
Permutation 9 : NTS = 1.0074336881229937
Permutation 10 : NTS = 1.0070910011818335
-----------------------------------
Broke file into 116,566 byte segments.
Tested 1,165,660 bytes for each compressor.
Using 3 compressors.
Minimum NTS = 1.0020026702269693
Maximum NTS = 1.0203881110292312
Mean NTS = 1.0077227212024413
0.00% unchanged by shuffle.
Probability of 30.0 heads and 0.0 tails = 0.0000
Reject Ho.  Not IID!

And the equivalent failure by the NIST ea_iid test:-

                statistic  C[i][0]  C[i][1]  C[i][2]
----------------------------------------------------
                excursion      16       0       6
       numDirectionalRuns       6       0      97
       lenDirectionalRuns     280       6       0
   numIncreasesDecreases*   10000       0       0
           numRunsMedian*   10000       0       0
            lenRunsMedian       8       5       1
             avgCollision     215       0       6
             maxCollision       5       1       7
          periodicity(1)*   10000       0       0
          periodicity(2)*   10000       0       0
          periodicity(8)*   10000       0       0
         periodicity(16)*   10000       0       0
         periodicity(32)*   10000       0       0
           covariance(1)*   10000       0       0
           covariance(2)*   10000       0       0
           covariance(8)*   10000       0       0
          covariance(16)*   10000       0       0
          covariance(32)*       0       0   10000
             compression*   10000       0       0
(* denotes failed test)

** Failed IID permutation tests

And the test for 10 MB of /dev/urandom, along with it’s text output:-

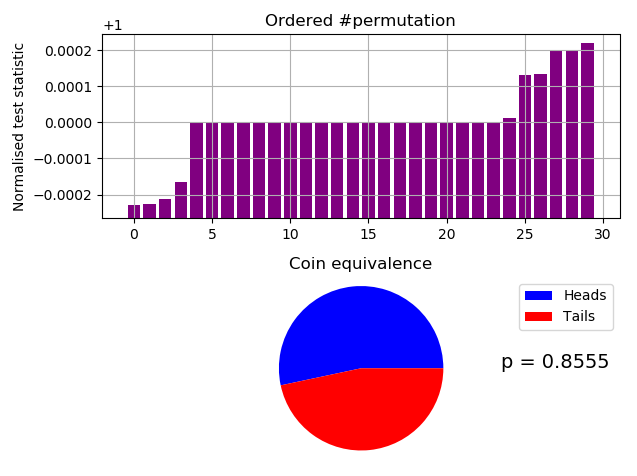
Successful test of 10 MB of /dev/urandom output.

Successful test of 10 MB of /dev/urandom output.

LZMA tests...
Permutation 1 : NTS = 1.0
Permutation 2 : NTS = 1.0
Permutation 3 : NTS = 1.0
Permutation 4 : NTS = 1.0
Permutation 5 : NTS = 1.0
Permutation 6 : NTS = 1.0
Permutation 7 : NTS = 1.0
Permutation 8 : NTS = 1.0
Permutation 9 : NTS = 1.0
Permutation 10 : NTS = 1.0


BZ2 tests...
Permutation 1 : NTS = 0.9997870273799193
Permutation 2 : NTS = 1.0001303342526375
Permutation 3 : NTS = 0.999773134102621
Permutation 4 : NTS = 1.00013433945291
Permutation 5 : NTS = 1.0001970804227474
Permutation 6 : NTS = 1.0000129395850772
Permutation 7 : NTS = 1.0002190303526288
Permutation 8 : NTS = 1.0002010500385679
Permutation 9 : NTS = 0.9997701032743862
Permutation 10 : NTS = 0.9998358009629029


ZLIB tests...
Permutation 1 : NTS = 1.0
Permutation 2 : NTS = 1.0
Permutation 3 : NTS = 1.0
Permutation 4 : NTS = 1.0
Permutation 5 : NTS = 1.0
Permutation 6 : NTS = 1.0
Permutation 7 : NTS = 1.0
Permutation 8 : NTS = 1.0
Permutation 9 : NTS = 1.0
Permutation 10 : NTS = 1.0
-----------------------------------
Broke file into 1,000,000 byte segments.
Tested 10,000,000 bytes for each compressor.
Using 3 compressors.
Minimum NTS = 0.9997701032743862
Maximum NTS = 1.0002190303526288
Mean NTS = 1.0000020279941466
66.67% unchanged by shuffle.
Probability of 16.0 heads and 14.0 tails = 0.8555
*** Accept Ho. The data file looks like IID ***

Conclusion

This and other ad-hoc testing of real world and synthetic data samples suggests that our two tests perform correctly. And by virtue of these, we can verify that NIST’s ea_iid also works correclty.